[Algorithm] 백준 2003 수들의 합 2 (C++)

2003번: 수들의 합 2

알고리즘 분류

• 브루트포스 알고리즘
• 두 포인터

문제 풀이

• 투포인터를 활용하는 문제
  • 2개의 포인터가 동시에 같은 위치에서 출발하는 문제다.
• 수열의 i번째 수부터 j번째 수까지의 합이 M이 되는 경우의 수를 구하면 된다.
  • 그렇기 때문에 2개의 포인터를 활용하고, 2개의 포인터가 같은 위치 (0번째 인덱스)에서 출발한다.
• 2개의 포인터 (leftPointer, rightPointer)가 0번째 인덱스에서 출발하고, 경우에 따라서 leftPointer, rightPointer를 이동시키면 된다.
• 조건
  • leftPointer는 항상 rightPointer보다 왼쪽에 있거나 같은 위치에 있어야한다. (leftPointer <= rightPointer)
  • rightPointer가 수열의 크기보다 큰 곳을 가리키면 탐색이 종료된다.(rightPointer != N)
• 구간의 합을 구하는 코드
• int sum = 0; for (int i = leftPointer; i <= rightPointer; i++) { sum += arr[i]; }
• 구간의 합 sum과 M 비교
  • sum > M
    • M보다 sum이 클 경우, leftPointer를 증가시킨다.
    • rightPoint를 증가시켜봤자, 이미 sum은 M을 넘기 때문에 의미가 없다.
    • 이 때 주의해야할 것이 있는데, leftPointer와 rightPointer가 같은 경우에는 leftPointer가 아닌 rightPointer를 증가시켜줘야한다. 그래야 leftPointer가 rightPointer를 역전하는 상황이 생기지 않는다.
  • sum < M
    • M보다 sum이 작을 경우, rightPointer를 증가시킨다.
    • rightPointer를 증가시킴으로써 sum이 M에 가깝게 해주려는 작업!
  • sum == M
    • answer를 1 증가시킨다. 그리고 rightPointer도 1 증가시킨다.
    • 구간에 숫자가 1개만 존재할 때 (leftPointer와 rightPointer가 가리키는 위치가 같을 경우), sum이 M을 만족하는 경우가 있을 수 있다. 만약 여기서 leftPointer를 증가시킨다면, 이 경우 또한 leftPointer가 rightPointer를 역전하는 상황이 되기 때문에, 무조건 rightPointer를 증가시켜야한다!

 

상세 풀이

두 포인터가 움직이는 과정을 보면 다음과 같다.

여기서 sum은 leftPointer부터 rightPointer 사이의 구간에 있는 배열의 원소들의 합이다.

 

1. 초기 상태, leftPointer의 인덱스 = 0, rightPointer의 인덱스 = 0

여기서 sum은 1으로 (연속구간이 1 부터 1), M (5)보다 작기 때문에 rightPointer를 증가시켜준다. 

sum이 더 커져야 하는 상황으로, rightPointer를 증가시킴으로써 연속 구간을 넓혀준다.

 

 

 

2. leftPointer의 인덱스 = 0, rightPointer의 인덱스 = 1

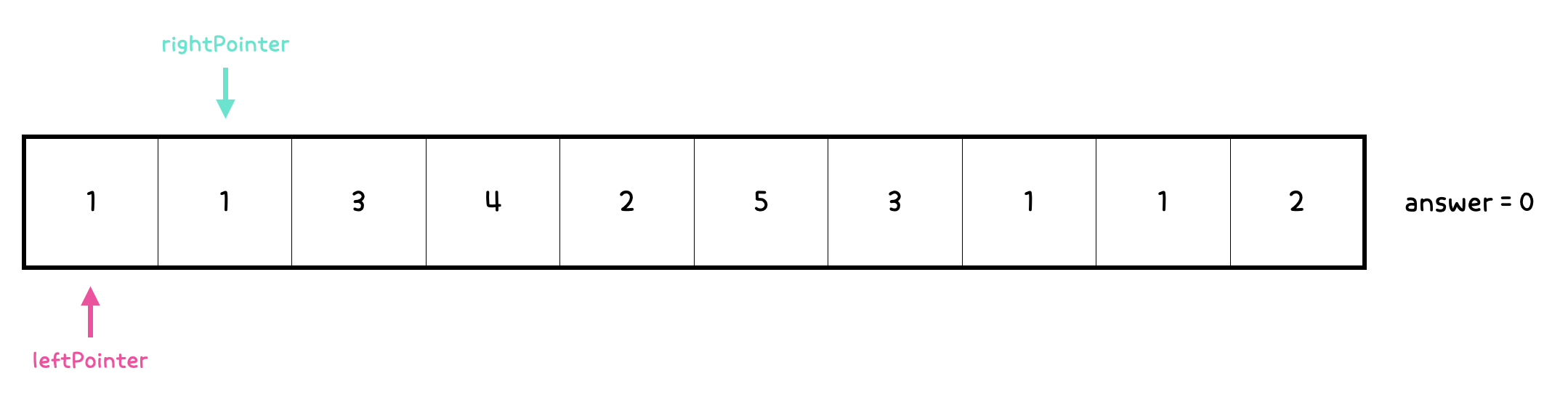
sum = 1 + 1 = 2로, M보다 작기 때문에 rightPointer를 증가시켜준다. (sum이 더 커져야 하는 상황)

 

 

3. leftPointer의 인덱스 = 0, rightPointer의 인덱스 = 2

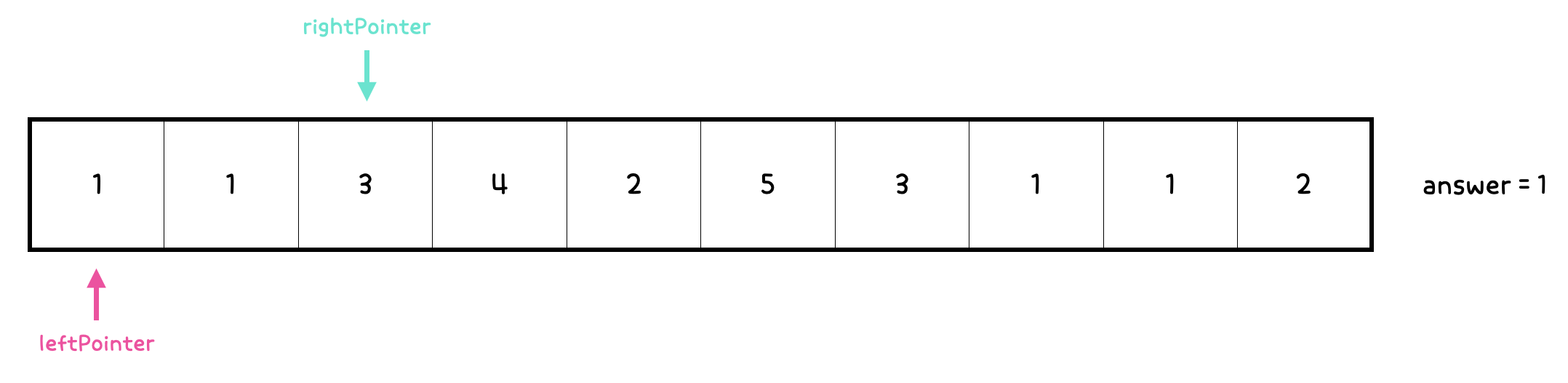
sum = 1 + 1 + 3 = 5로, M과 같은 값이기 때문에 answer를 1 증가시키고 rightPointer를 증가시킨다.

이 때 같은 값인데 하필 rightPointer를 증가시키는 이유는,

위의 풀이에서 말했던 것처럼 구간에 숫자가 1개만 존재할 경우, leftPointer를 증가시키게 되면 leftPointer가 rightPointer를 역전하는 상황이 오기 때문에 while 문의 조건을 벗어나게 된다. 

지금의 상황에서는 구간의 숫자가 여러 개이기 때문에 leftPointer를 증가시켜도 되지만, 숫자가 1개만 존재한다면 무조건 rightPointer를 증가시켜야 한다.

 

 

4. leftPointer의 인덱스 = 0, rightPointer의 인덱스 = 3

sum = 1 + 1 + 3 + 4 = 9로, sum이 M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 줄여야 하는 상황)

이 때 rightPointer를 증가시키지 않는 이유는, 

이미 sum이 M보다 크기 때문에, 만약 rightPointer를 증가시키게 되면 구간을 더 늘리게 되는 것이기 때문에 어차피 또 sum은 M보다 큰 값이 되기 때문이다.

그래서 leftPointer를 증가시킴으로써 연속 구간을 줄여주고, sum을 줄인다.

 

 

5. leftPointer의 인덱스 = 1, rightPointer의 인덱스 = 3

sum = 1 + 3 + 4 = 8로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

 

6. leftPointer의 인덱스 = 2, rightPointer의 인덱스 = 3

sum = 3 + 4 = 7로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

7. leftPointer의 인덱스 = 3, rightPointer의 인덱스 = 3

sum = 4로, M보다 작기 때문에 rightPointer를 증가시킨다. (sum을 증가시켜야 하는 상황)

현재 leftPointer == rightPointer인데 이 때 만약 rightPointer가 아닌 leftPointer를 증가시키게 되면,

leftPointer가 rightPointer를 역전하는 상황이 발생한다.

그렇기 때문에 leftPointer == rightPointer인 경우에는 rightPointer를 증가시킨다.

 

 

8. leftPointer의 인덱스 = 3, rightPointer의 인덱스 = 4

sum = 4 + 2 = 6로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

 

9. leftPointer의 인덱스 = 4, rightPointer의 인덱스 = 4

sum = 2로, M보다 작기 때문에 rightPointer를 증가시킨다. (sum을 증가시켜야 하는 상황)

 

 

10. leftPointer의 인덱스 = 4, rightPointer의 인덱스 = 5

sum = 2 + 5 = 7로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

 

11. leftPointer의 인덱스 = 5, rightPointer의 인덱스 = 5

sum = 5로, M과 같으므로 rightPointer를 증가시킨다. 

answer도 1 증가시킨다.

 

 

12. leftPointer의 인덱스 = 5, rightPointer의 인덱스 = 6

sum = 5 + 3 = 8로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

 

13. leftPointer의 인덱스 = 6, rightPointer의 인덱스 = 6

sum = 3로, M보다 작기 때문에 rightPointer를 증가시킨다. (sum을 증가시켜야 하는 상황)

 

 

14. leftPointer의 인덱스 = 6, rightPointer의 인덱스 = 7

sum = 3 + 1 = 4로, M보다 작기 때문에 rightPointer를 증가시킨다. (sum을 증가시켜야 하는 상황)

 

 

 

15. leftPointer의 인덱스 = 6, rightPointer의 인덱스 = 8

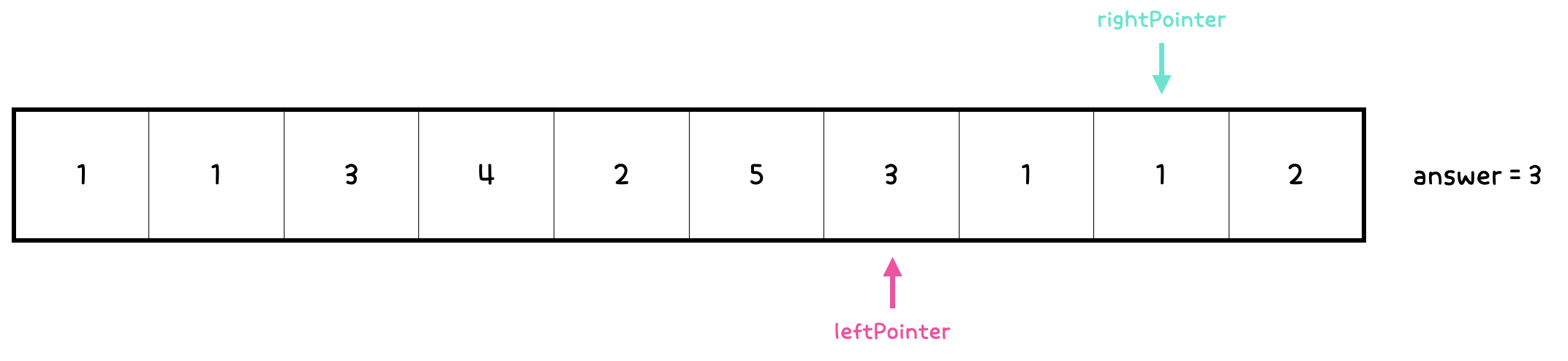
sum = 3 + 1 + 1 = 5로, M과 같으므로 rightPointer를 증가시킨다.

answer도 1 증가시킨다.

 

 

16. leftPointer의 인덱스 = 6, rightPointer의 인덱스 = 9

sum = 3 + 1 + 1 + 2 = 7로, M보다 크기 때문에 leftPointer를 증가시킨다. (sum을 감소시켜야 하는 상황)

 

 

17. leftPointer의 인덱스 = 7, rightPointer의 인덱스 = 9

sum = 1 + 1 + 2 = 4로, M보다 작기 때문에 rightPointer를 증가시켜야 한다. (sum을 증가시켜야 하는 상황)

근데 rightPointer는 더이상 갈 곳이 없기 때문에 여기서 끝이다!

 

 

반례

4 1
1 1 1 1
답 4

4 1
1 2 3 1
답 2

소스 코드 (C++)

//  수들의 합 2
//  2003.cpp
//  Algorithm
//
//  Created by 안상희 on 2023/05/01.
//

#include <iostream>

using namespace std;

int N, M; // N개로 이루어진 수열의 합이 M이 되는 경우의 수를 구하기!

int main() {
  cin.tie(0);
  cout.tie(0);
  std::ios::sync_with_stdio(false);
  
  cin >> N >> M;
  int arr[N];
  
  for (int i = 0; i < N; i++) {
    cin >> arr[i];
  }
  
  int leftPointer = 0;
  int rightPointer = 0;
  int answer = 0;
  
  while (leftPointer <= rightPointer && rightPointer != N) {
    int sum = 0;
    for (int i = leftPointer; i <= rightPointer; i++) {
      sum += arr[i];
    }
    
    if (sum > M) {
      // M보다 합이 클 경우, leftPointer 증가시키기. rightPoint를 증가시켜봤자 이미 M을 넘기 때문에 의미가 없다.
      // leftPointer와 rightPointer가 같은 경우에는, left가 아닌 right를 증가시켜줘야 역전하는 상황이 생기지 않는다.
      if (leftPointer == rightPointer) { rightPointer++; }
      else { leftPointer++; }
    } else if (sum < M) {
      // M보다 합이 작을 경우, rightPointer 증가시키기
      rightPointer++;
    } else {
      answer++;
      rightPointer++; // rightPointer 증가시켜야함!
//      leftPointer++; 구간에 숫자가 1개만 존재할 때 (leftPointer와 rightPointer가 가리키는 위치가 같을 경우), sum이 M을 만족하는 경우가 있을 수 있다. 만약 여기서 leftPointer를 증가시킨다면, 이 경우 또한 leftPointer가 rightPointer를 역전하는 상황이 되기 때문에, 무조건 rightPointer를 증가시켜야한다!
    }
  }
  
  cout << answer << '\\n';
  return 0;
}